Como Foi Criada?

A fórmula de Bhaskara foi demonstrada pelo matemático Bhaskara II no século XII. Ele era um renomado matemático e astrônomo que contribuiu significativamente para a matemática e ciências astronômicas da Índia medieval. Vale ressaltar que, embora tenha a fórmula tenha seu nome como homenagem, não foi Bhaskara II que a criou, pois acredita-se que a fórmula ja era conhecida antes.

A fórmula de Bhaskara é derivada principalmente de uma técnica conhecida como complementar o quadrado. Abaixo está um resumo do processo até chegar na fórmula que conhecemos atualmente:

1. Começamos com a forma geral de uma equação quadrática:

   

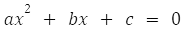
2. Após isso, movemos o termo constante c para outro lado da equação:

   

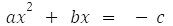
3. Agora iremos dividir ambos os lados da equação por a para simplificar futuros cálculos, assumindo que a seja diferente de zero:

   

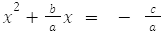
4. Para completar o quadrado, adicionamos o quadrado do quarto do coeficiente de x elevado ao quadrado nos dois lados da equação:

   

5. Feito isso, o lado esquerdo da equação pode ser reescrito como um quadrado perfeito:

   

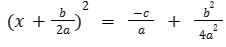
6. Agora, iremos extrair a raíz quadrada em ambos os lados:

   

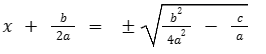
7. Na raíz iremos calcular o múltiplo comum dos denominadores e teremos o este resultado:

   

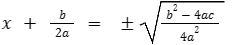
8. Usando o a propriedade de radiação (extrair raíz quadrada de uma divisão é a mesma coisa que fazer a raíz quadrada do numerador pelo denominador):

   

   Porém, nota-se que 4a² é um quadrado perfeito e com isso podemos tirar a raíz, resultando em: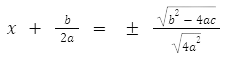

   

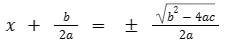
9. Feito isso, iremos passar b/2a para o lado direito da equação, deixando apenas o x no lado esquerdo:

   

   Para ficar mais organizado, iremos deixar tudo no mesmo denomidador e, finalmente, teremos nossa fórmula de bhaskara!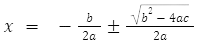

   

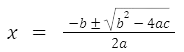
Como Chegar no Resultado

1. Primeiro precisamos calcular o descriminante (delta) como base nos coeficientes fornecidos (a, b e c):

   delta = b² - 4.a.c

   delta = ?

2. Para continuar certifique-se de fornecer os coeficientes da função